II-4. Notice 1 : Deviner le nombre choisi

Notice 1

Devinez le nombre choisi

1°. Analyse du problème.

Les lampes $X$ , $Y$ , $Z$ , éteintes ou allumées, doivent indiquer le nombre choisi, de 0 à 7, en système binaire. Ainsi :

( $X=0$ , $Y =0$ , $Z=0$ ) correspond à zéro ;
( $X=0$ , $Y =0$ , $Z=1$ ) correspond à 1 ;
( $X=0$ , $Y=1$ , $Z=0$ ) correspond à 2 ;
…
( $X=1$ , $Y =1$ , $Z=1$ ) correspond à 7.

Or à chaque nombre choisi correspond une suite de trois 0 ou 1 correspondants aux réponses données aux trois questions posées.

2° Table de valeurs.

– Si 0 est le nombre choisi, les réponses aux questions posées sont : « oui », « oui », « oui », c’est-à-dire $A = 1$ , $B = 1$ , $C = 1$ .

– Si 1 est le nombre choisi, les réponses aux questions posées sont : « non », « oui », « oui », c’est-à-dire $A=0$ , $B = 1$ , $C = 1$ .
– En étudiant les huit cas possibles, on obtient la table de valeurs ci-dessous.

$\begin{tabular}{|c|c|c||c|c|c||c|} \multicolumn{3}{c}{\textsf{\large{}$\begin{array}{c} entr\acute{e}e\\ \overbrace{\qquad\qquad} \end{array}$}} & \multicolumn{4}{c}{\textsf{\large{}$\begin{array}{c} sortie\\ \overbrace{\qquad\qquad\qquad} \end{array}$}}\tabularnewline \hline \textsf{\large{}A} & \textsf{\large{}B} & \textsf{\large{}C} & \textsf{\large{}X} & \textsf{\large{}Y} & \textsf{\large{}Z} & % \begin{minipage}[c]{10mm}% \noindent \begin{center} nombre \par\end{center} \noindent \begin{center} choisi\\ ~ \par\end{center}% \end{minipage}\tabularnewline \hline 1 & 1 & 1 & 0 & 0 & 0 & 0\tabularnewline \hline 0 & 1 & 1 & 0 & 0 & 1 & 1\tabularnewline \hline 1 & 1 & 0 & 0 & 1 & 0 & 2\tabularnewline \hline 0 & 1 & 0 & 0 & 1 & 1 & 3\tabularnewline \hline 1 & 0 & 0 & 1 & 0 & 0 & 4\tabularnewline \hline 0 & 0 & 0 & 1 & 0 & 1 & 5\tabularnewline \hline 1 & 0 & 1 & 1 & 1 & 0 & 6\tabularnewline \hline 0 & 0 & 1 & 1 & 1 & 1 & 7\tabularnewline \hline \end{tabular}$

3° Expressions algébriques.

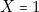La lampe $X$ doit être allumée ( $X=1$ ) lorsque (lignes 4 à 8 de la table) : 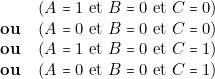$\begin{tabular}{cc} & ($A=1$ et $B=0$ et $C=0$) \tabularnewline \textbf{ou} & ($A=0$ et $B=0$ et $C=0$) \tabularnewline \textbf{ou} & ($A=1$ et $B=0$ et $C=1$) \tabularnewline \textbf{ou} & ($A=0$ et $B=0$ et $C=1$) \tabularnewline \end{tabular}$ ce qui correspond à : 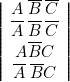$\left|\begin{array}{c} A\;\overline{B}\;\overline{C}\\ \overline{A}\;\overline{B}\;\overline{C}\\ A\overline{B}C\\ \overline{A}\;\overline{B}C \end{array}\right| \qquad$ Donc, on écrit :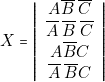 $X=\left|\begin{array}{c} A\overline{B}\;\overline{C}\\ \overline{A}\;\overline{B}\;\overline{C}\\ A\overline{B}C\\ \overline{A}\;\overline{B}C \end{array}\right|$
On montre de même (lignes 3, 4, 7, 8 de la table de vérité) que :
$Y=\left|\begin{array}{c} AB\overline{C}\\ \overline{A}B\overline{C}\\ A\overline{B}C\\ \overline{A}\;\overline{B}C \end{array}\right|$
De même (lignes 2, 4, 6, 8 de la table) :
$Z=\left|\begin{array}{c} \overline{A}BC\\ \overline{A}B\overline{C}\\ \overline{A}\;\overline{B}\;\overline{C}\\ \overline{A}\;\overline{B}C \end{array}\right|$

4° Simplifications. (Voir 1re partie, paragraphes 6 et 7).

Pour $X$ :
$X=\left|\begin{array}{c} A\;\overline{B}\;\overline{C}\\ \overline{A}\;\overline{B}\;\overline{C}\\ A\overline{B}C\\ \overline{A}\;\overline{B}C \end{array}\right|=\left|\begin{array}{c} \left|\begin{array}{c} A\\ \overline{A} \end{array}\right|\overline{B}\;\overline{C}\\ \left|\begin{array}{c} A\\ \overline{A} \end{array}\right|\overline{B}C \end{array}\right|=\left|\begin{array}{c} \overline{B}\;\overline{C}\\ \overline{B}C \end{array}\right|=\left|\overline{B}\left|\begin{array}{c} \overline{C}\\ C \end{array}\right|\right|=\overline{B}$
De même :
$Y=\left|\begin{array}{c} B\overline{C}\left|\begin{array}{c} A\\ \overline{A} \end{array}\right|\\ \overline{B}C\left|\begin{array}{c} A\\ \overline{A} \end{array}\right| \end{array}\right|=\left|\begin{array}{c} B\;\overline{C}\\ \overline{B}C \end{array}\right|$
De même :
$Z=\left|\begin{array}{c} \overline{A}B\left|\begin{array}{c} C\\ \overline{C} \end{array}\right|\\ \overline{A}\;\overline{B}\left|\begin{array}{c} C\\ \overline{C} \end{array}\right| \end{array}\right|=\left|\begin{array}{c} \overline{A}B\\ \overline{A}\;\overline{B} \end{array}\right|=\left|\overline{A}\left|\begin{array}{c} B\\ \overline{B} \end{array}\right|\right|=\overline{A}$

Donc $X=\overline{B}$ ; $Y=\left|\begin{array}{c} B\;\overline{C}\\ \overline{B}C \end{array}\right|$ ; $Z=\overline{A}$

5° Schéma du programme. (voir notice $\framebox{1}$ ).

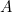Nous avons choisi la colonne 2 pour « alimenter » la lampe $X$ . Sur cette colonne 2, $A$ est « neutralisée » en plaçant les deux fiches indiquées ; de même pour 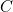$C$ . La fiche enfoncée dans la barrette 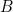$B$ , correspond à $B$ . D’où cette colonne 2 « représente $\overline{B}$ ».
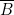Pour alimenter la lampe 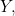$Y,$ « nous fait \textbf{deux} colonnes de programmation. Nous avons chois les colonnes 3 et 5. La colonne 3, avec ses fiches en place, correspond à 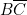$B\overline{C}$ et la colonne 5 à $\overline{B}C$ .
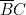Pour « alimenterv » la lampe 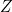$Z$ , il faut une colonne de programmation. Nous avons choisi, la colonne 6. Elle représente, lorsque les fiches sont en place, $\overline{A}$ .
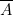Ainsi se trouve justifié le programme présenté sur la notice $\framebox{1}$ .